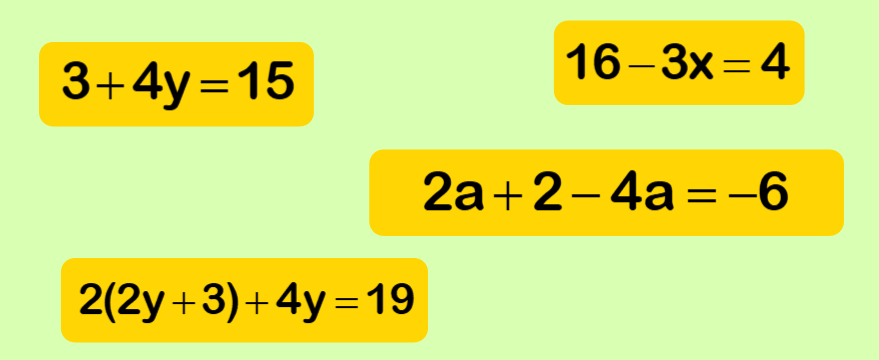Equations Worksheets – New & Engaging
Equations Worksheets
What Are Linear Equations?
Students learn how to solve equations from year 7 onward. Solving equations ranges in difficulty. Students may understand how to manipulate algebraic expressions before they are ready to solve equations.
Linear Equations Example 1
The image below shows different examples of linear equations.
2c = 4 is different to x - 5 = -1. With the equation 2c = 4 we divide both sides by 2. The answer is c = 2. With x - 5 = -1 we add (-5) to both sides. The answer is x = 4 because -1 + (-5) equals 4.
Linear Equations Example 2
The linear equation examples below are more tricky.
To solve the equation 2a + 2 - 4a = - 6, we first collect like terms. 2a - 4a is -2a. The equation becomes 2 - 2a = - 6. Next we subtract 2 from both sides. The equation becomes - 2a = - 8. Next we divide both sides by negative 2. We are left with an answer of a = 4.
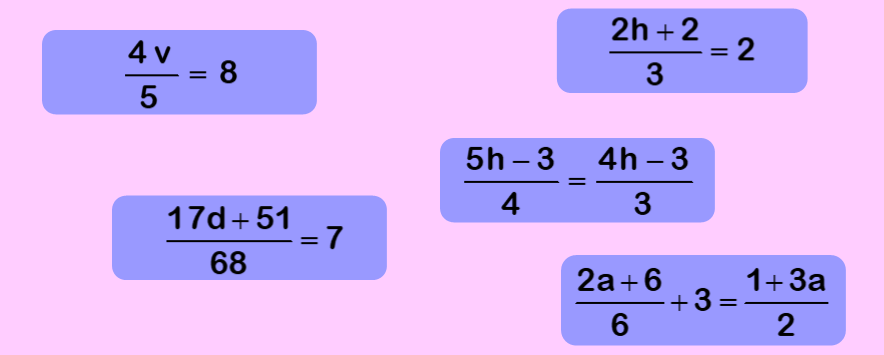
Linear Equations Example 3
The equations below involve division and or fractions. In the case of 4v / 5 = 8 we first multiply both sides by 5. Next we divide both sides by 4. The final answer is v = 10. We can always substitute the final answer into the original equation to see if it is correct.
How do You Calculate An Equation?
Equations is a GCSE Foundation and GCSE Higher topic. Experienced teachers will have their own unique approach when teaching how to solve equations. We recommend the balancing method as this is a common way to introduce the topic solving equations. As prerequisite topics we suggest: simplifying expressions, or substituting into expressions.
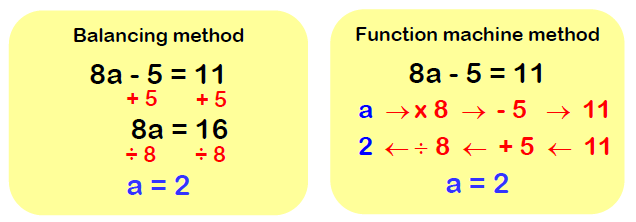
Balancing Method vs Function Machine Method
The image below shows an example of the balancing method as well as the function machine method. The equation 8a - 5 = 11 has been solved using the balancing method and the function machine method. a is the subject of the equation.
The final answer is a = 2.
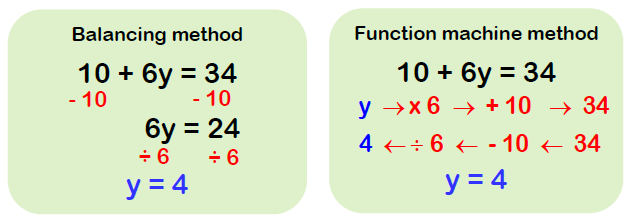
In the example below the equation 10 + 6y = 34 has been solved using the balancing method and the function machine method. y is the subject of the equation.
The final answer is y = 4.
In the example below the equation x/12 - 5 =4 has been solved using the balancing method and the function machine method. x is the subject of the equation.
The final answer is x = 108.