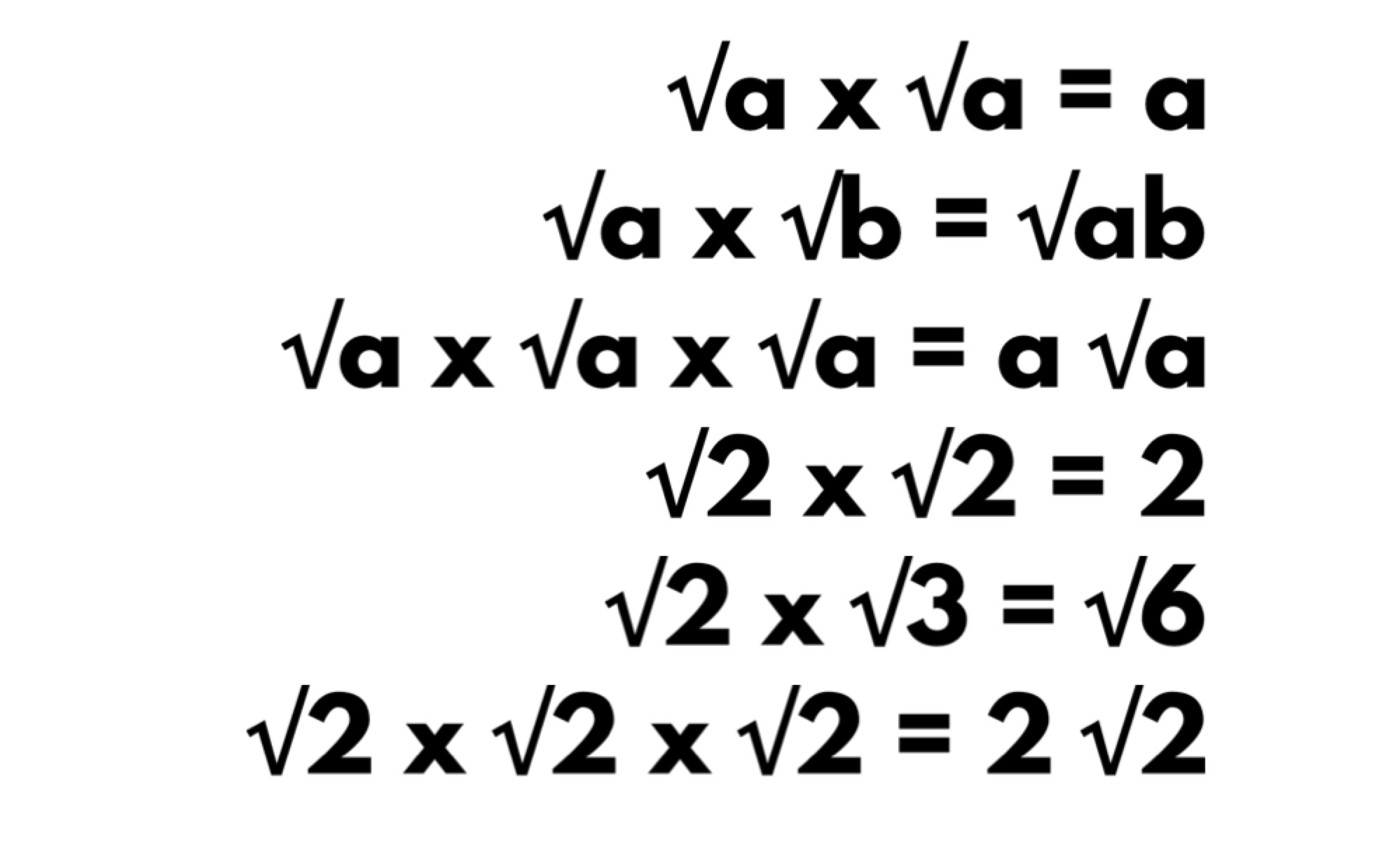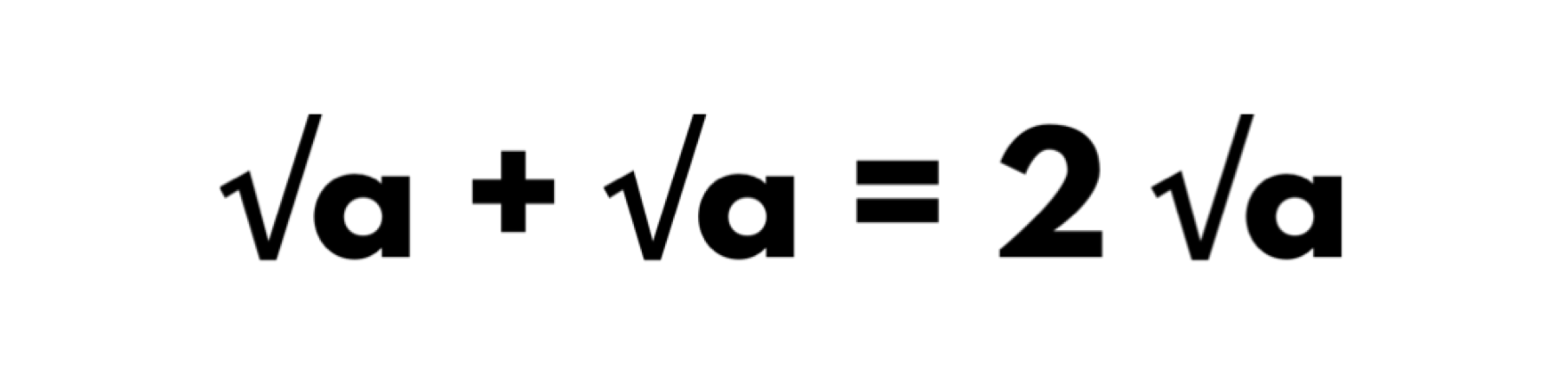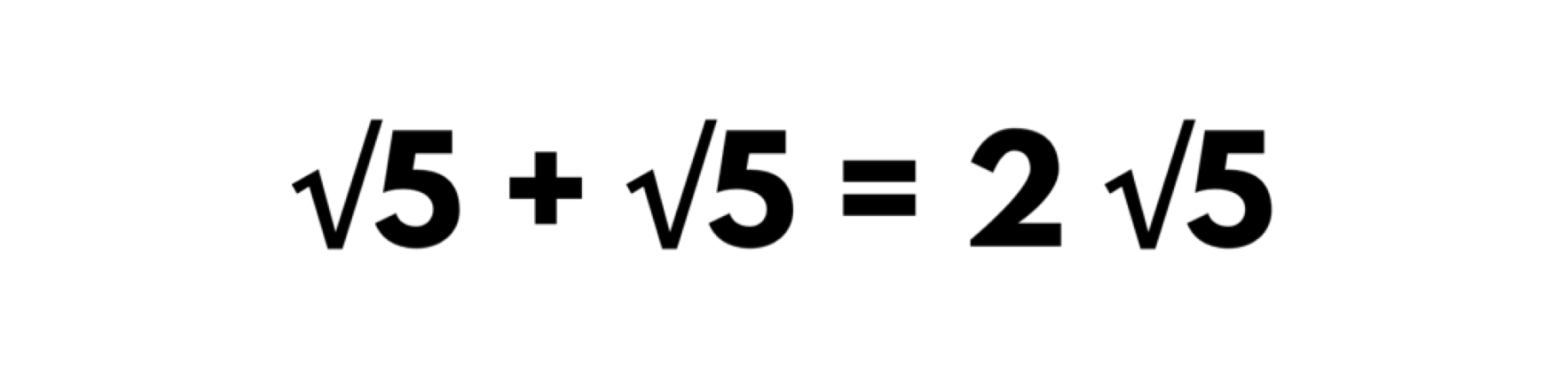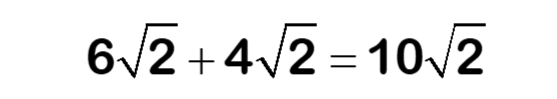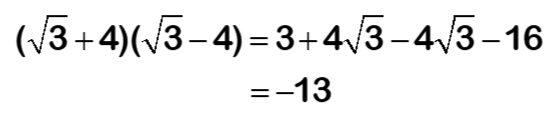Surds Worksheets – New & Engaging
Surds Worksheets
Laws of Surds
Indices and Index Notation follow specific laws. Surds also have rules. The graphic below shows how to add, subtract and multiply surds.
What are Surds?
A surd is an irrational number - it cannot be written as the fraction a/b where a and be are integers. Surds are written with a √ symbol. √2 is a surd for example, expressed as “root 2”. The example below shows division rules for Surds such that √2 ÷ √3 is written as √2/√3. Notice that √2/√3 is not a fraction in the form a/b where a and b are integers - a whole number, and b is non-zero.


The example below shows √3 ÷ √2.


The example below shows √5 + √5.
Simplifying Surds
Just like simplifying expressions, Surds can be simplified. The rules are similar to collecting like terms. The question below shows 6√2 + 4√2.
The question below shows √5 + 2√5 + 3√5.
The question below shows √40 when simplified as a surd.
The question below expands brackets when (√3 + 4)(√3 - 4). This technique is common when rationalising the denominator.
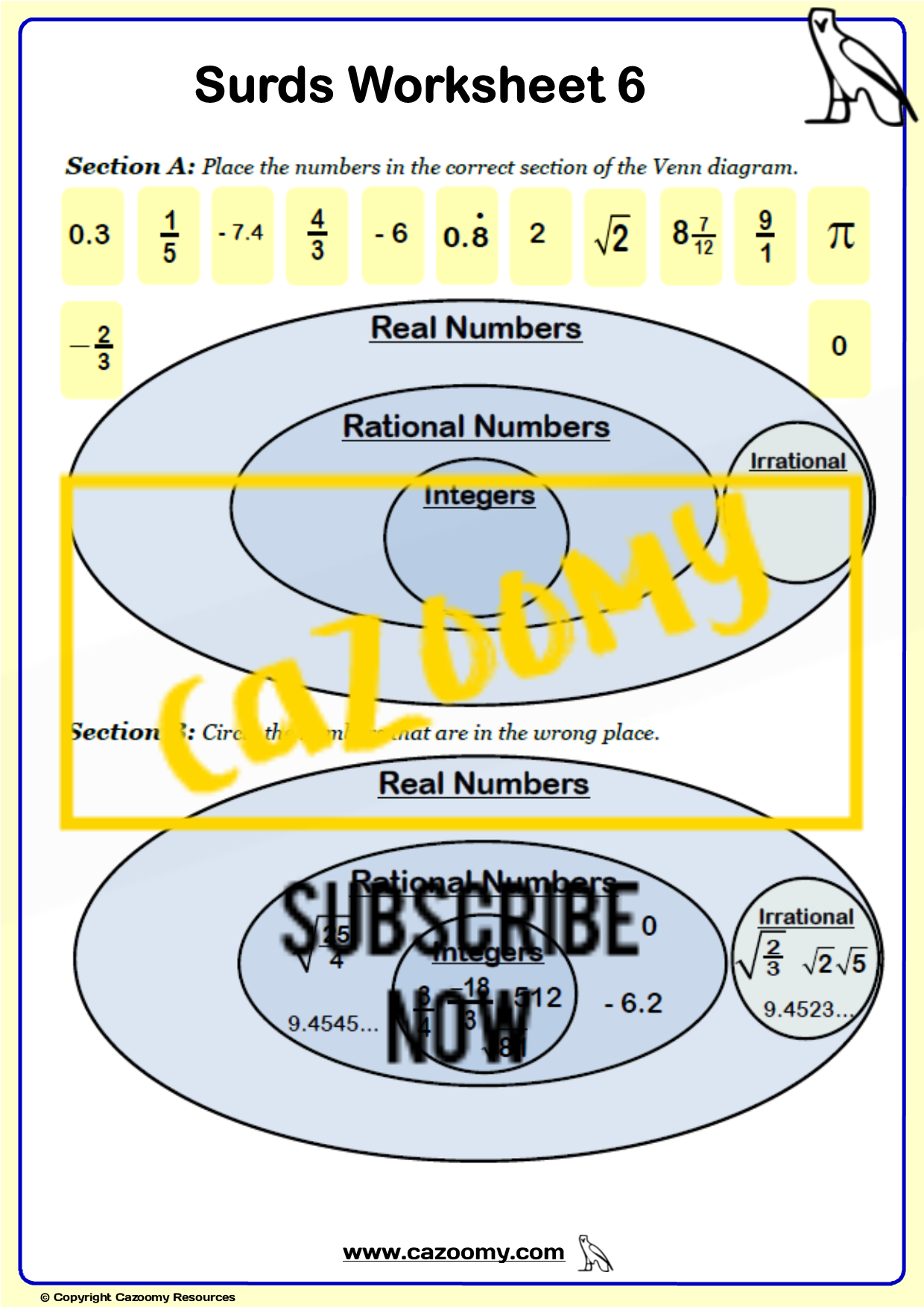
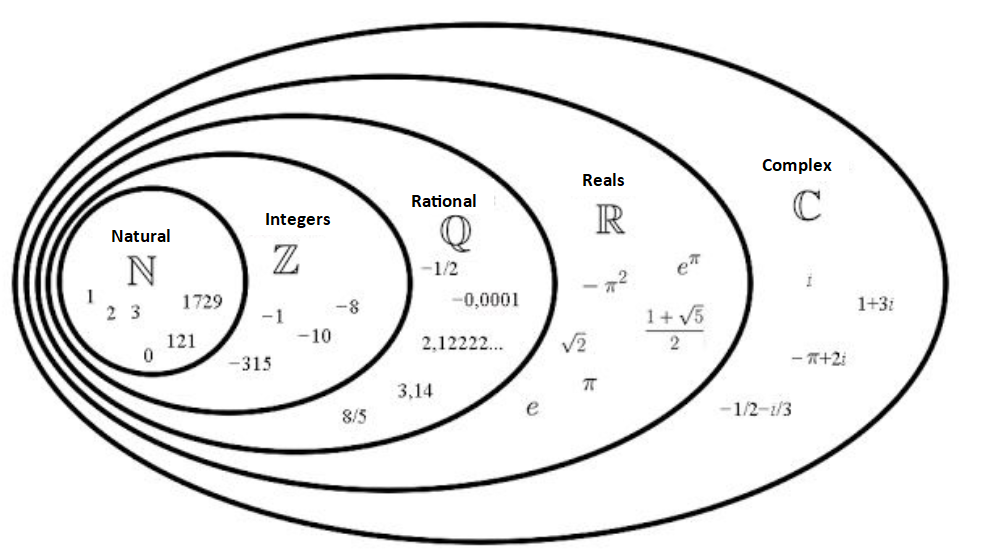
Rational Numbers
The graphic below shows the real number system. The inner numbers include natural numbers including zero, integers which include negative numbers, rational numbers which include fractions, real numbers including surds and complex numbers.