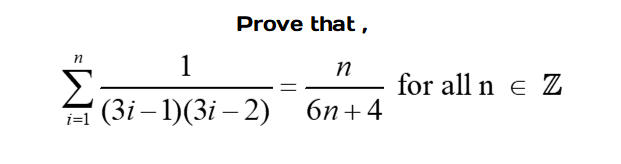Algebraic Proof Worksheets – New & Engaging
Algebraic Proof Worksheets
Algebraic Proof Written as Expressions
Algebraic Proof statements can be written as expressions usually using the letter "n". In the graphic below there are 6 statements that can written as an expression of n.
Algebraic Proof Example Question
The algebraic proof example below asks students to prove that the difference between 812 and 127 is a multiple of 4. To answer this question first show that 812 is the same as 81 x 811 which is the same as (4 x 2 x 811). Next show that 127 is the same as 121 x 126 which is the same as (4 x 3 x 126). As an extension to this problem students could show that the diference between 8a and 12b necessarily equals 4n.
'Prove that!'
Consider the conjecture below. Use proof by mathematical induction to come up with a solution.
Algebraic Proof Key Words
Terminology is important when applying algebraic proof. You'll want to have a good grasp of all the key words.
When proving a statement algebraically you will use expressions usually in the form of the letters n or x. For example, to prove that a number is even we show that n is divisible by 2, or that n is a multiple of 2.